Paper Notes - Vision Transformer

An Image is Worth 16x16 Words: Transformers for Image Recognition at Scale

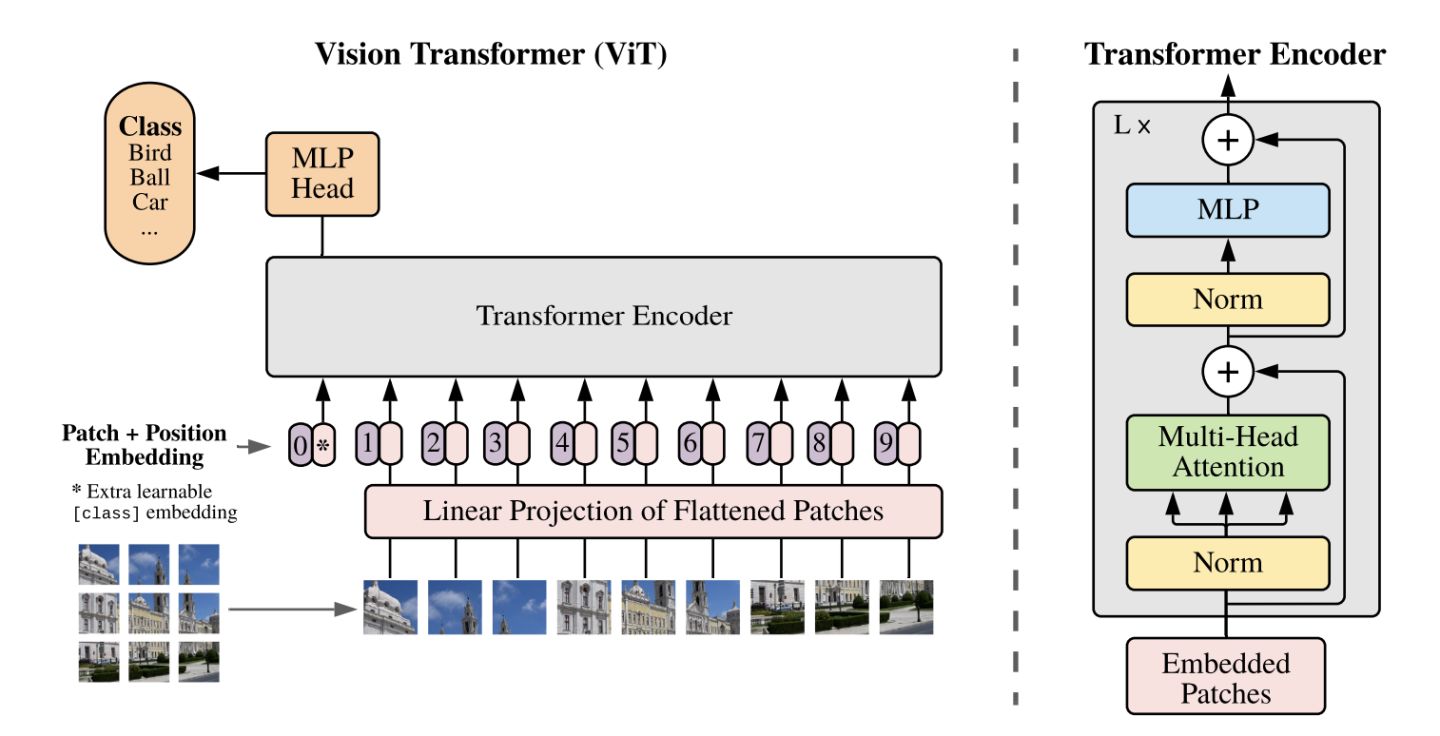
在整体的实现上, 原文完全使用原始bert的transformer结构, 主要是对图片转换成类似token的处理, 原文引入了一个patch的概念, 即将输入图片划分为一个个的patch, 然后对于每一个patch转换 (主要是flatten操作), 转换成类似bert的输入结构. 整体的框架如下图所示:

图像块嵌入 (Patch Embeddings)

标准 Transformer 接受一维标记嵌入序列 (Sequence of token embeddings) 作为输入. 为处理 2D 图像, 将图像 reshape 为一个展平 (flatten) 的 2D 块序列 $x_p\in \mathbb{R}^{N\times(P^2 \cdot C)}$, 其中 $H\times W$ 是原始图像的分辨率, $C$ 是通道数 (RGB 图像 $C=3$), $P^2$ 是每个图像块的分辨率, $N=HW/P^2$ 是产生的图像块数, 即 Transformer 的有效输入序列长度.

Transformer 在其所有层中使用恒定的隐向量 (latent vector) 大小 $D$, 因此我们将图像块展平, 并使用 FC 层将维度 $P^2 \cdot C$ 映射为 $D$ 维, 同时保持图像块数 $N$ 不变. 此投影输出称为图像块嵌入 (Patch Embeddings) (本质就是对每一个展平后的 patch vector $x_p\in \mathbb{R}^{N\times(P^2 \cdot C)}$ 做一个线性变换 / 全连接层 $E\in \mathbb{R}^{(P^2 \cdot C)\times D}$, 由 $P^2 \cdot C$ 维降维至 $D$ 维, 得到 $x_pE\in \mathbb{R}^{N\times D}$), 这好比于 NLP 中的词嵌入 (Word Embeddings).

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32


class PatchEmbed(nn.Module):
""" Image to Patch Embedding """

def __init__(self, img_size=224, patch_size=16, in_chans=3, embed_dim=768):
    super().__init__()
    # (H, W)
    img_size = to_2tuple(img_size)
    # (P, P)
    patch_size = to_2tuple(patch_size)
    # N = (H // P) * (W // P)
    num_patches = (img_size[1] // patch_size[1]) * (img_size[0] // patch_size[0])

    self.img_size = img_size
    self.patch_size = patch_size
    self.num_patches = num_patches

    # 可训练的线性投影 - 获取输入嵌入
    self.proj = nn.Conv2d(in_chans, embed_dim, kernel_size=patch_size, stride=patch_size)

def forward(self, x):
    B, C, H, W = x.shape
    # FIXME look at relaxing size constraints

    assert H == self.img_size[0] and W == self.img_size[1], \
        f"Input image size ({H}*{W}) doesn't match model ({self.img_size[0]}*{self.img_size[1]})."

    # (B, C, H, W) -> (B, D, (H//P), (W//P)) -> (B, D, N) -> (B, N, D)
    #   D=embed_dim=768, N=num_patches=(H//P)*(W//P)
    #   torch.flatten(input, start_dim=0, end_dim=-1)  # 形参: 展平的起始维度和结束维度    
    # 可见 Patch Embedding 操作 3 步到位
    x = self.proj(x).flatten(2).transpose(1, 2)
    return x

可学习的嵌入 (Learnable Embedding)

类似于 BERT 的 [class] token, 此处为图像块嵌入序列预设一个可学习的嵌入$z^0_0=x_{class}$, 该嵌入在 Transformer 编码器输出的状态/特征$z_L^0$用作图像表示$y$. $$ \begin{aligned} &z_0 = [x_{class}, x_p^1E, x_p^2E, …, x_p^NE] + E_{pos}\ &z_l' = MSA(LN(z_{l-1})) + z_{l-1}\ &z_l = MLP(LN(z_l'))+z_l'\ &y = LN(z_L^0) \end{aligned} $$ 无论是预训练还是微调, 都有一个分类头 (Classification Head) 附加在$z_L^0$之后, 从而用于图像分类. 分类头在预训练时由一个单层 MLP 实现, 在微调时由单个线性层实现 (多层感知机与线性模型类似, 区别在于 MLP 相对于 FC 层数增加且引入了非线性激活函数, 例如 FC + GELU + FC 形式的 MLP).

更明确地, 上式中给长度为$N$的嵌入向量后追加了一个分类向量, 用于训练 Transformer 时学习类别信息. 假设将图像分为 $N$ 个图像块, 输入到 Transformer 编码器中就有 $N$ 个向量, 但该取哪一个向量用于分类预测呢? 一个合理的做法是手动添加一个可学习的嵌入向量作为用于分类的类别向量$x_{class}$, 同时与其他图像块嵌入向量一起输入到 Transformer 编码器中, 最后取追加的首个可学习的嵌入向量作为类别预测结果. 所以, 追加的首个类别向量可理解为其他个图像块寻找的类别信息. 从而最终输入 Transformer 的嵌入向量总长度为$N+1$. 可学习嵌入在训练时随机初始化, 然后通过训练得到, 其具体实现为:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20


### 随机初始化
self.cls_token = nn.Parameter(torch.zeros(1, 1, embed_dim))  # shape = (1, 1, D)

### 分类头 (Classifier head)
self.head = nn.Linear(self.num_features, num_classes) if num_classes > 0 else nn.Identity()

### 前馈过程 (Forward)
B = x.shape[0]  # Batch Size

# 通过 可学习的线性投影 获取 Input Imgaes 的 Patch Embeddings (实现在 3.1 节)
x = self.patch_embed(x)  # x.shape = (B, N, D)

# 可学习嵌入 - 用于分类
cls_tokens = self.cls_token.expand(B, -1, -1)  # shape = (B, 1, D)

# 按元素相加 附带 Position Embeddings
x = x + self.pos_embed  # shape = (B, N, D) - Python 广播机制

# 按通道拼接 获取 N+1 维 Embeddings
x = torch.cat((cls_tokens, x), dim=1)  # shape = (B, N+1, D)

位置嵌入 (Position Embeddings)

位置嵌入 $E_{pos}\in\mathbb{R}^{(N+1)\times D}$ 也被加入图像块嵌入, 以保留输入图像块之间的空间位置信息. 不同于 CNN, Transformer 需要位置嵌入来编码 patch tokens 的位置信息, 这主要是由于自注意力的扰动不变性 (Permutation-invariant), 即打乱 Sequence 中 tokens 的顺序并不会改变结果.

相反, 若不给模型提供图像块的位置信息, 那么模型就需要通过图像块的语义来学习拼图, 这就额外增加了学习成本. ViT 论文中对比了几种不同的位置编码方案:

无位置嵌入
1-D 位置嵌入: 考虑把 2-D 图像块视为 1-D 序列
2-D 位置嵌入: 考虑图像块的 2-D 位置 (x, y)
相对位置嵌入: 考虑图像块的相对位置

最后发现如果不提供位置编码效果会差, 但其它各种类型的编码效果效果都接近, 这主要是因为 ViT 的输入是相对较大的图像块而非像素, 所以学习位置信息相对容易很多.

Transformer 原文中默认采用固定位置编码, ViT 则采用标准可学习/训练的 1-D 位置编码嵌入, 因为尚未观察到使用更高级的 2-D-aware 位置嵌入能够带来显著的性能提升. 在输入 Transformer 编码器之前直接将图像块嵌入和位置嵌入按元素相加:

1
2
3
4
5
6


# 多 +1 是为了加入上述的 class token
# embed_dim 即 patch embed_dim
self.pos_embed = nn.Parameter(torch.zeros(1, num_patches + 1, embed_dim)) 

# patch emded + pos_embed : 图像块嵌入 + 位置嵌入
x = x + self.pos_embed

Transformer 编码器

Transformer 编码器由交替的多头自注意力层 (MSA, 附录 A) 和多层感知机块 (MLP, 等式 2, 3) 构成. 在每个块前应用层归一化 (Layer Norm), 在每个块后应用残差连接 (Residual Connection).

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31


# MHA
class Attention(nn.Module):
    def __init__(self, dim, num_heads=8, qkv_bias=False, qk_scale=None, attn_drop=0., proj_drop=0.):
        super().__init__()

        self.num_heads = num_heads
        head_dim = dim // num_heads

        self.scale = qk_scale or head_dim ** -0.5

        self.qkv = nn.Linear(dim, dim * 3, bias=qkv_bias)
        self.attn_drop = nn.Dropout(attn_drop)
        self.proj = nn.Linear(dim, dim)

        # 附带 dropout
        self.proj_drop = nn.Dropout(proj_drop)

    def forward(self, x):
        B, N, C = x.shape
        qkv = self.qkv(x).reshape(B, N, 3, self.num_heads, C // self.num_heads).permute(2, 0, 3, 1, 4)
        q, k, v = qkv[0], qkv[1], qkv[2]  # make torchscript happy (cannot use tensor as tuple)

        attn = (q @ k.transpose(-2, -1)) * self.scale
        attn = attn.softmax(dim=-1)
        attn = self.attn_drop(attn)

        x = (attn @ v).transpose(1, 2).reshape(B, N, C)
        x = self.proj(x)
        x = self.proj_drop(x)

        return x

在 Transformer中, MSA 后跟一个 FFN (Feed-forward network), 其包含两个 FC 层, 第一个 FC 将特征从维度变换成 , 第二个 FC 将特征从维度恢复成 , 中间的非线性激活函数均采用 GeLU (Gaussian Error Linear Unit, 高斯误差线性单元) —— 这实质是一个 MLP (多层感知机与线性模型类似, 区别在于 MLP 相对于 FC 层数增加且引入了非线性激活函数, 例如 FC + GeLU + FC), 实现如下:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19


class Mlp(nn.Module):
def __init__(self, in_features, hidden_features=None, out_features=None, act_layer=nn.GELU, drop=0.):
    super().__init__()

    out_features = out_features or in_features
    hidden_features = hidden_features or in_features
    self.fc1 = nn.Linear(in_features, hidden_features)
    self.act = act_layer()
    self.fc2 = nn.Linear(hidden_features, out_features)
    self.drop = nn.Dropout(drop)

def forward(self, x):
    x = self.fc1(x)
    x = self.act(x)
    x = self.drop(x)
    x = self.fc2(x)
    x = self.drop(x)

    return x

一个 Transformer Encoder Block 就包含一个 MSA 和一个 FFN, 二者都有跳跃连接和层归一化操作构成 MSA Block 和 MLP Block, 实现如下:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27


# Transformer Encoder Block
class Block(nn.Module):
    def __init__(self, dim, num_heads, mlp_ratio=4., qkv_bias=False, qk_scale=None, drop=0., attn_drop=0.,
                drop_path=0., act_layer=nn.GELU, norm_layer=nn.LayerNorm):
        super().__init__()

        # 后接于 MHA 的 Layer Norm
        self.norm1 = norm_layer(dim)
        # MHA
        self.attn = Attention(dim, num_heads=num_heads, qkv_bias=qkv_bias, 
                            qk_scale=qk_scale, attn_drop=attn_drop, proj_drop=drop)
        # NOTE: drop path for stochastic depth, we shall see if this is better than dropout here
        self.drop_path = DropPath(drop_path) if drop_path > 0. else nn.Identity()

        # 后接于 MLP 的 Layer Norm
        self.norm2 = norm_layer(dim)
        # 隐藏层维度
        mlp_hidden_dim = int(dim * mlp_ratio)
        # MLP
        self.mlp = Mlp(in_features=dim, hidden_features=mlp_hidden_dim, act_layer=act_layer, drop=drop)

    def forward(self, x):
        # MHA + Add & Layer Norm
        x = x + self.drop_path(self.attn(self.norm1(x)))
        # MLP + Add & Layer Norm
        x = x + self.drop_path(self.mlp(self.norm2(x)))
        return x

集合了类别向量、图像块嵌入和位置编码三者到一体的输入嵌入向量后, 即可馈入Transformer Encoder. ViT 类似于 CNN, 不断前向通过由 Transformer Encoder Blocks 串行堆叠构成的 Transformer Encoder, 最后提取可学习的类别嵌入向量 —— class token 对应的特征用于图像分类.

归纳偏置与混合架构

归纳偏置 (Inductive bias): 注意到, Vision Transformer 的图像特定归纳偏置比 CNN 少得多. 在 CNN 中, 局部性、二维邻域结构和平移等效性存在于整个模型的每一层中. 而在 ViT 中, 只有 MLP 层是局部和平移等变的, 因为自注意力层都是全局的. 二维邻域结构的使用非常谨慎: 在模型开始时通过将图像切分成块, 并在微调时调整不同分辨率图像的位置嵌入. 此外, 初始化时的位置嵌入不携带有关图像块的 2D 位置的信息, 图像块之间的所有空间关系都必须从头开始学习.

混合架构 (Hybrid Architecture): 作为原始图像块的替代方案, 输入序列可由 CNN 的特征图构成. 在这种混合模型中, 图像块嵌入投影 $E$ 被用在经 CNN 特征提取的块而非原始输入图像块. 作为一种特殊情况, 块的空间尺寸可以为 $1\times 1$, 这意味着输入序列是通过简单地将特征图的空间维度展平并投影到 Transformer 维度获得的. 然后, 如上所述添加了分类输入嵌入和位置嵌入, 再将三者组成的整体馈入 Transformer 编码器. 简单来说, 就是先用 CNN 提取图像特征, 然后由 CNN 提取的特征图构成图像块嵌入. 由于 CNN 已经将图像降采样了, 所以块尺寸可为 $1\times 1$.

An Image is Worth 16x16 Words: Transformers for Image Recognition at Scale#

An Image is Worth 16x16 Words: Transformers for Image Recognition at Scale